Solve the system using the substitution method:
Step 1: Use either equation and solve for a variable.
In this case, we solved the first equation for y.
Step 2: Substitute the resulting quantity into the other equation.
Here we substituted the quantity found for y into the second equation.
Step 3: Solve for the remaining variable.
Step 4: Back substitute to find the value for the other variable.
Step 5: Present your answer as an ordered pair (x, y).It does not matter if you choose to solve for x or y first. However, make sure that you do not substitute into the same equation in step 2.
Instructional Video: Solving Systems of Equations using Substitution
Solve the system using the substitution method:
Solve for y in the first equation.
Any true statement, including 0 = 0, indicates a dependent system.
The next system consists of two parallel lines which has no simultaneous solution.
Solve the system using the substitution method:
Solve for x in the first equation.
Any false statement indicates an inconsistent system.
Solve the systems using the substitution method.
Typical word problem: When Joe walked away from the craps table he had 45 chips. He had a combination of $5 and $25 chips that added to a total of $625. How many of each chip did he have?
Set up a system of two linear equations.
Solve the system.
Answer: Joe had 25 five-dollar chips and 20 twenty-five dollar chips.
Video Examples on YouTube:









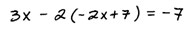






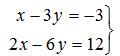












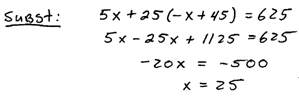


comment 0 التعليقات:
more_vertsentiment_satisfied Emoticon