Solve.
Not all equations work out to have a single solution. Some have infinitely many solutions such as x = x. Here any number the we chose for x will produce a true statement. Also, some equations have no solution such as x + 1 = x.
Contradiction – An equation that will always be false has no solution.
Identity – An equation that will always be true has any real number, R, as a solution.
It is quite common to encounter linear equations that require us to distribute before combining like terms.
Solve.
Literal equations are difficult for many people because there will be more than one variable. Just remember that the letters are place holders for some number, so the steps for solving are the same. Isolate the variable that it asks us to solve for.
Video Examples on YouTube:







Contradiction – An equation that will always be false has no solution.
Identity – An equation that will always be true has any real number, R, as a solution.
It is quite common to encounter linear equations that require us to distribute before combining like terms.
Solve.
Literal equations are difficult for many people because there will be more than one variable. Just remember that the letters are place holders for some number, so the steps for solving are the same. Isolate the variable that it asks us to solve for.
Word Problem: The internet connection at the hotel costs $5.00 to log on and $0.20 a minute to access. If Joe's total bill came to $18.00 then how many minutes did Joe spend on the internet? (Set up an algebraic equation and solve it)
Video Examples on YouTube:







J. Redden on G+


















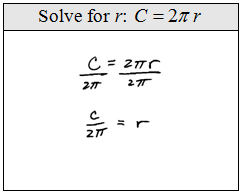







comment 0 التعليقات:
more_vertsentiment_satisfied Emoticon