- Look to factor out any GCF.
- Four-Term Polynomials - Factor by grouping.
- Trinomials - Factor using the "guess and check" method.
- Binomials - Use the the special products in this order:
Sum and Difference of Squares
Sum and Difference of Cubes
* If a binomial is both a difference of squares and cubes, then to obtain a more complete factorization, factor it as a difference of squares first.
* Not all polynomials factor. In this case, beginning algebra students may write, "does not factor - DNF."Factor.
Tip: Make some note cards to aid in helping memorize the formulas for the special products. Look for factors to factor further - sometimes factoring once is not enough.
Factor.
Take some time to understand the difference between the last two solved problems. Notice that x^6 - y^6 is both a difference of squares and a difference of cubes at the same time. Here we chose to apply the difference of squares formula first. On the other hand, for x^6 + y^6 we chose to apply the sum of cubes formula first because it does not factor as a sum of squares.
Factor.
Video Examples on YouTube: Factor the following polynomials.
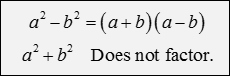








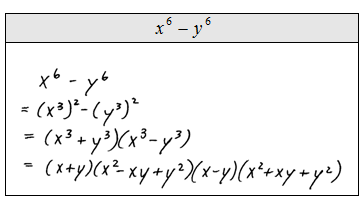














comment 0 التعليقات:
more_vertsentiment_satisfied Emoticon