Vertical Translations: [ Interactive Graph ]
If k is any positive real number then,
The graph of the basic function f(x) = sqrt(x) follows:
Using this basic graph and the vertical translations described above we can sketch f(x) = sqrt(x) + 2 by shifting all of the points up 2 units. Similarly, graph g(x) = sqrt(x) − 3 by shifting all points down 3 units.
Horizontal Translations: [ Interactive Graph ]
Using the graph of f(x) = sqrt(x) and the horizontal translations described above we can sketch f(x) = sqrt(x + 4) by shifting all of the points left 4 units. Similarly, graph g(x) = sqrt(x − 3) by shifting all points right 3 units.
Reflections: [ Interactive Graph ]
Given any function f(x),
Using the graph of f(x) = sqrt(x) sketch the graph of f(x) = −sqrt(x) by reflecting all of the points about the x-axis. Similarly, graph f(x) = sqrt(−x) by reflecting all of the points about the y-axis.


For the first function f(x) = −sqrt(x) all of the y-values are negative which results in a reflection about the x-axis. For the second function f(x) = sqrt(−x) all of the x-values must be negative thus resulting in a reflection about the y-axis.
Sketch the graph.
The -1 indicates a reflection of the graph of the squaring function f(x) = x^2 about the x-axis. Be sure to graph the squaring function using a dashed curve because it will be used as a guide and is not the answer. Next, reflect all points about the x-axis and draw in the final graph with a solid curve.
General Steps for Graphing Functions using Transformations:
1. Identify and graph the basic function using a dashed curve.
2. Identify any reflections first and sketch them using the basic function as a guide.
3. Identify any translations.
4. Use this information to sketch the final graph using a solid curve.
Graph the function and determine the domain and range.
Use the transformations to determine the equation that represents the given function.Example:
From the general shape of the graph we can determine the basic function and transformations. The graph has the shape of the square root function,
y = sqrt(x)
Next, notice the reflection about the y-axis,y = sqrt(−x)
And finally, we see a shift up 1 unit.y = sqrt(−x) + 1
Example:
The given function has the general shape of the squaring function (parabola),
y = x^2
Next, notice the shift right 3 units,y = (x − 3)^2
And finally, we see a shift down 2 units.y = (x − 3)^2 − 2
Example:
The given function has the general shape of the absolute value function,
y = abs(x)
Next, notice the reflection about the x-axis,y = −abs(x)
Finally we see a shift left 1 unit and down 2 unitsy = −abs(x+1) − 2
You Tube Videos:
































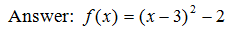





comment 0 التعليقات:
more_vertsentiment_satisfied Emoticon